地震長期予測モデルをシミュレーションしてみた#1 An illustrative visualisation of a Brownian model for recurrent earthquakes #1

This article contains the following topics;

  • Implementation of a simple Brownian passage time model (BPT model) for recurrent earthquakes with Plotly and JavaScript.
  • Illustration of the relationship between a Brownian motion and an Inverse Gaussian distribution, underlying a BPT model.

本記事では次のトピックを扱います。
・地震の長期予測モデル（BPTモデル）をJavascriptとPlotlyで簡単に実装します。
・BPTモデルの基礎となっている、ウィーナー過程の初期通過時間と逆ガウス分布の関係をシミュレーションで明らかにします。

Preface はじめに

Some types of stochastic processes (e.g. a Poisson process/a Brownian process) are used for long-term seismic forecasting of earthquakes. The Brownian process (BPT model) is applied for recurrent earthquakes, whereas the Poisson process is for non-recurring earthquakes.
地震の長期予測ではBPTモデルやポアソン過程モデルなど、確率過程を基礎とするモデルが用いられています。BPTモデルは主要活断層帯の地震や海溝型地震など、繰り返し発生する地震の予測に利用されており、ポアソン過程モデルは過去の最新活動時期が不明の地震の予測に利用されています。

With a BPT model, intervals between earthquakes are assumed to follow an Inverse Gaussian distribution. This article demonstrates a simple BPT model with Plotly and Javascript, and also illustrates the characteristics of Inverse Gaussian distribution.
BPTモデルでは地震の発生間隔は逆ガウス分布（BPT分布、Brownian Passage Time Distribution）に従うと仮定されます。この記事ではPlotlyとJavascriptを用いて簡単にBPTモデルをシミュレーションし、逆ガウス分布の性質を確認してみます。

Overview of the BPT model モデルの概要

The BPT model introduces a Brownian motion and reflects the macromechanics of stress and strain accumulation, which is said to cause recurrent earthquakes according to the plate tectonics theory. Let {\displaystyle X_{t} \\\ } be a Brownian motion with drift and scaling. {\displaystyle X_{t} \\\ } consists of the two terms as shown below, the one with drift parameter \mu \\\ and the other with scale parameter \sigma \\\ and standard Brownian motion {\displaystyle B_{t} \\\ }. An earthquake is assumed to occur when this {\displaystyle X_{t} \\\ } reaches a critical failure threshold (let this threshold be a \\\ ).
{\displaystyle X_{0}=0 \\\ }
{\displaystyle X_{t}=\mu t+\sigma B_{t} \\\ }
{\displaystyle T_{n}\sim Inverse Gaussian Dist\left( \dfrac{ a }{\mu },\left( \dfrac{ a }{\sigma }\right) ^{2}\right) \\\ }

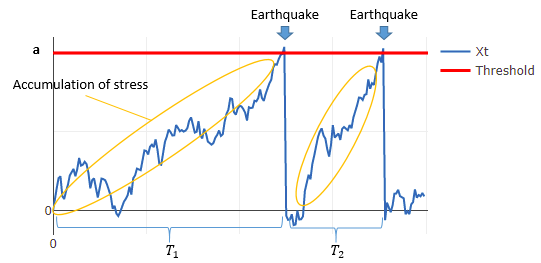
f:id:r_std:20210522183741p:plain
Time series of Xt

プレート境界で発生する地震は、プレート運動により蓄積した応力が地震によって解放されることで発生すると考えられています。BPTモデルではこの応力の蓄積と解放という地震発生の物理的過程を、ブラウン運動を用いた更新過程で表現します。

確率過程{\displaystyle X_{t} \\\ }は時間比例で増加するドリフト項部分{\displaystyle \mu t \\\ }とブラウン運動部分{\displaystyle \sigma B_{t} \\\ }で表現されます。（{\displaystyle B_{t} \\\ }は標準ブラウン運動）
BPTモデルではこの{\displaystyle X_{t} \\\ }を用いてプレートに蓄積した応力を表現します。{\displaystyle X_{t} \\\ }が一定の閾値 a \\\ を超過すると地震が発生します。地震によって応力が解放されると{\displaystyle X_{t} \\\ }は０に戻る、というモデル化を行っています。
上記の条件の下では、地震の発生間隔が逆ガウス分布に従うことが分かっていますが、本当にそうなるでしょうか？シミュレーションで検証してみます。

Simulation with Plotly and Javascript 実装

Assumption 計算前提

Simulation period シミュレーション年数：
Threshold 閾値： a =\\\
Drift ドリフト ： \mu =\\\
Scaling 分散： \sigma =\\\

Simulation results シミュレーション結果

Please note that "Expected" in the chart above is not equal to a pdf of an Inverse Gaussian distribution. To make the orange curve of "Expected" comparable to the histogram of "Observed", the bin width of the histogram is multiplied to the pdf of the expected distribution.

The relationship between a Brownian motion and an Inverse Gaussian distribution ウィーナー過程と逆ガウス分布の関係性

Based on the simulation results above, the intervals between earthquakes seem to follow an Inverse Gaussian distribution. (The analytic solution is to be added.)
シミュレーションの結果から確かに発生間隔が逆ガウス分布に従うことが確認できました。
以下、ウィーナー過程（Brown運動）と逆ガウス分布の関係性を解析的に解きます。（追記予定）

Reference in Japanese 参考文献、サイト

地震調査研究推進本部 全国地震動予測地図２０２０年版 地震動予測地図の解説編
https://www.jishin.go.jp/main/chousa/20_yosokuchizu/yosokuchizu2020_tk_3.pdf

『地震発生の長期予測モデルについて』 東北大学耐震工学研究会
http://drdm.irides.tohoku.ac.jp/taishin/pdf/shibata_paper_20th.pdf

Source code

github.com

javascriptで花火を打ち上げてみた

例のウィルスで各地の花火大会が軒並み中止になってしまったので、javascriptで花火をシミュレーションしてみます。

f:id:r_std:20200817085617j:plain

※上記画像はあくまでイメージです

完成物

 

全画面表示はこちら→https://fireworks-2020.glitch.me/

BGMが強制再生される仕様ですが、環境によっては再生されないためご注意ください。

 

 

使用したサービス、参考サイトなど

Glitch


自前でサーバーやドメインを用意せずとも、js, css, htmlを無料で公開することができるサービスです。
glitch.com

Coding Challenge


様々なテーマでサンプルコードを紹介しているサイトです。Youtubeの解説動画が大変参考になります。有志が作成したサンプルコードも共有されているので、いろいろなコードを比較することができます。
thecodingtrain.com

 

感想

次回はThree.jsやWebGLを用いて３D化を試みます。

天鳳位の成績データを統計的に分析してみた

麻雀 データサイエンス

本記事では天鳳位15名の方（2020年5月現在）の牌譜データを分析します。現環境の麻雀強者たちにどのような打ち筋・タイプがあるかを明らかにし、plotyを用いた3D表示を試みます。

１．使用データ

オンライン対戦麻雀 天鳳 / ランキングで牌譜データが公開されている15名の天鳳位の方（※）の成績データを使用します。
（※ASAPIN氏、（≧▽≦）氏、独歩氏、すずめクレイジー氏、太くないお氏、タケオしゃん氏、コーラ下さい氏、かにマジン氏、就活生@川村軍団氏、ウルトラ立直氏、トトリ先生19歳氏、おかもと氏、gousi氏、お知らせ氏、右折するひつじ氏。以下、敬称略。なお、トトリ先生19歳氏はASAPIN氏のサブアカウント、右折するひつじ氏はおかもと氏のサブアカウントのようです。打ち手が同じ場合に打ち筋の評価がどう変化するのかどうか注目です。）

なお、部屋は鳳凰卓のみ、ルールは東南戦(喰アリ赤アリ)を対象としています。

集計後の成績データについては次のリンクをご覧ください。今回は全データのうち、11変数（※）を抽出して分析します。
(※トップ率、ラス率、和了率、和了素点、和了平均巡目、和了時平均ドラ数、放銃率、放銃素点、リーチ率、1副露率、2副露率）
github.com
Tenhoui_ALL.csv

２．分析手法

以前の記事と同様に因子分析（プロマックス回転）を用いて分析します。分析手法の詳細は前記事をご覧ください。
r-std.hatenablog.com

３．分析結果

３．１．因子負荷量

f:id:r_std:20200530150050p:plain
因子分析の結果
第三因子までの累積寄与率は0.773となり、第三因子までで分析対象の11変数の概ねを表すことができます。
打ち筋の1つ目の軸は仕掛け派⇔手作り派であると言えます。第一因子の因子負荷量が示すとおり、副露を多用して安手を上がるタイプと、副露は多用せずドラを絡めて高い手を狙うタイプがあります。
打ち筋の2つ目の軸はリスク愛好派⇔リスク回避派です。第二因子の因子負荷量のとおり、放銃率・ラス率が高い積極的なタイプとこれらを低く抑える保守的なタイプがあります。
打ち筋の3つ目の軸はリーチ派⇔ダマ派です。リーチを多用し放銃素点も高いタイプ、リーチを使わず放銃素点が低いタイプがあります。

３．２．Plotlyを用いた3D plot

天鳳位の15名の成績データをもとに散布図を描いてみると、次のとおりになります。

 
明らかなクラスタリングを見ることはできませんが、打ち手によって個性があることが見てとれます。

例えば、お知らせ氏は第三因子得点が大きく、リーチを多用する打ち筋であると評価できます。実際のリーチ率は19.7％と天鳳位の中でも高い水準にあります。
また、すずめクレイジー氏は第二因子得点が小さく、リスク回避派な打ち筋であると評価できます。実際の放銃率は10.6％、ラス率も20.1％と天鳳位の中ではかなり低い水準のようです。
（≧▽≦）氏は第一因子得点が大きく、仕掛け派であることがわかります。実際の副露率は40.5％とかなり高めです。

初代天鳳位のASAPIN氏は局当たり収支が天鳳位中でトップである等の好成績を残していますが、打ち筋としては天鳳位の中では標準的なポジションに位置しているようです。また、サブアカウントのトトリ先生19歳氏はASAPIN氏と比較すると、第一因子得点が大きいことが分かります。（オリジナルは実際の副露率が35.9％であるのに対し、サブアカウントでは39.6%とかなり高い水準になっています。）
一方で、おかもと氏と右折するひつじ氏のプロットは非常に近い位置になっており、サブアカウントでも打ち筋が大きく変化していないものと思われます。

４．まとめ

・天鳳位の打ち筋の軸として、次の3つが考えられます。
　①仕掛け派⇔手作り派
　②リスク愛好派⇔リスク回避派
　③リーチ派⇔ダマ派
・天鳳位の方々の成績データには明らかなクラスタリングは見られないものの、因子分析を利用してプレーヤーの特徴・打ち筋をある程度表現することが可能なようです。

ソースコードなどはこちらにまとめています。
github.com

（関連記事）
r-std.hatenablog.com
r-std.hatenablog.com

「アクチュアリー試験の合格率を予測してみた」を検証してみた

アクチュアリー試験

この記事は過去記事の検証を行います。

r-std.hatenablog.com

前の記事では2019年度アクチュアリー１次試験の合格率と受験者数を予測してみましたが、今回は当時の予測がどの程度予測が当たっていたかを検証してみます。

 

１．アクチュアリー１次試験の合格率予測の検証

各科目の合格率の予実差は次のとおりとなりました。

　　　 数学 生保 損保 年金 KKT
実績 23.9% 32.0% 16.2% 17.0% 22.1%
予想 16.5% 18.3% 18.3% 19.2% 22.4%
予実差 7.4pt 13.7pt -2.1pt -2.2pt -0.3pt

生保と数学の実際の合格率がやや高くなりました。

前回と同様に、ロジット変換後の合格率が定常な正規分布に従うと仮定すると、2019年度の合格率実績のPercentileは次のとおりとなります。

logit\left( pass\_ rate_{subject,year}\right) \sim N\left( \mu_{subject} ,\sigma_{subject} ^{2}\right)
 
  数学 生保 損保 年金 KKT
Percentile 75.5% 84.8% 39.6% 42.7% 48.5%

当たり前の結果ではありますが、合格率を1点で読みに行くことはやはり難しいことが分かります。

なお、直近の2019年度の合格率も含めた推移は次のとおりです。

f:id:r_std:20200324085259p:plain

2001~2019年の合格率の推移

 2010~2019

  H22 H23 H24 H25 H26 H27 H28 H29 H30  
  2010 2011 2012 2013 2014 2015 2016 2017 2018 2019
数学 11.9% 11.1% 46.8% 18.4% 26.5% 20.2% 19.7% 10.3% 13.0% 23.9%
生保 35.3% 12.6% 49.2% 26.5% 10.2% 14.0% 10.6% 26.2% 12.8% 32.0%
損保 12.8% 10.5% 39.9% 30.1% 22.6% 20.5% 13.2% 13.7% 23.5% 16.2%
年金 11.6% 8.1% 46.8% 58.2% 10.2% 18.5% 16.6% 16.4% 35.2% 17.0%
KKT 18.8% 20.5% 47.6% 20.3% 22.0% 46.1% 17.2% 19.0% 14.1% 22.1%

2001~2009

  H13 H14 H15 H16 H17 H18 H19 H20 H21
  2001 2002 2003 2004 2005 2006 2007 2008 2009
数学 9.7% 17.1% 17.7% 6.8% 7.2% 10.6% 41.8% 22.8% 18.9%
生保 29.5% 9.7% 22.5% 7.0% 10.2% 11.0% 38.7% 21.9% 21.5%
損保 29.6% 15.2% 18.1% 22.7% 9.9% 11.9% 13.1% 36.6% 10.5%
年金 14.5% 19.5% 12.4% 11.4% 18.9% 11.9% 52.0% 18.1% 11.6%
KKT 17.6% 34.3% 30.1% 11.5% 23.0% 15.3% 24.8% 27.1% 15.1%

 

 

２．アクチュアリー１次試験の受験者数の検証

各科目の受験者数の予実差は次のとおりとなりました。

  数学 生保 損保 年金 KKT
実績 1,136 774 637 442 725
予想 1,021 747 663 486 735
予実差 +115 +27 -26 -44 -10

数学の受験者数は予実差が大きいことが分かります。前回の記事では、直近年度の各５科目の受験者数と合格者数を変数とするモデルを作成しましたが、数学だけはあてはまりが良くなかったようです。

数学はエントリー科目としての要素が強いので、他の科目の受験者数・合格者数情報は使用しない方が良いかもしれないという仮説を立てモデルを作り直すと、2019年の数学の予想受験者数は1,126人となり、もう少し改善の余地があるようです。

 

３．結論

予測が外れても問題ないように、しっかり勉強・準備しておくことが大切です。

 

2019年度の試験情報をアップデートしたデータは次のとおりです。

github.com

コピュラを可視化してみた An illustrative visualisation of Copula

アクチュアリー試験 損保数理

This article gives you an intuitive, visual guide to copula with javascript and plotly.
本記事ではコピュラの確率密度関数を3D plotで可視化してみます。損保数理や金融機関のリスク管理、デリバティブのプライシング等でおなじみのコピュラですが、javascriptとplotlyを用いて表現するとどうなるでしょうか。標準正規分布の確率密度関数も同時に図示して、コピュラの種類やパラメータを変更した際の挙動についても確認してみます。

f:id:r_std:20200209200802p:plain
An example of
Frank Copula density

コピュラの種類　Types of Copulas


共単調コピュラ Minimum copula
反単調コピュラ Maximum copula
積コピュラ Independence copula
フランクコピュラ Frank copula
ガンベルコピュラ Gumbel copula
クレイトンコピュラ Clayton copula
正規コピュラ Gaussian copula
tコピュラ t copula

計算前提　Assumptions

アルキメデスコピュラのパラメータ　Parameter for Archimedean Copula

\alpha =\\\

正規コピュラ、tコピュラのパラメータ　Parameters for Gaussian & t Copula

\rho\\\ (correlation coefficient) =
\eta\\\ (degree of freedom) =

プロット実行　Plot densities

ボタンを順番に押すとplotが表示されます。


実行結果　Results

相関係数と裾従属係数 Correlation Coefficient and Tail Dependency

Kendall's tauUpper tail dependencyLower tail dependency

そもそもコピュラって？　What is Copula?

コピュラは複数の確率変数の同時確率を表現するのに用いられます。例えば2つ一組のサイコロを振る場合、何の変哲もない独立なサイコロと必ずゾロ目が出るギャンブラーのサイコロは次のとおりの同時確率となります。

何の変哲もない独立なサイコロ

  1 2 3 4 5 6 計
1 1/36 1/36 1/36 1/36 1/36 1/36 1/6
2 1/36 1/36 1/36 1/36 1/36 1/36 1/6
3 1/36 1/36 1/36 1/36 1/36 1/36 1/6
4 1/36 1/36 1/36 1/36 1/36 1/36 1/6
5 1/36 1/36 1/36 1/36 1/36 1/36 1/6
6 1/36 1/36 1/36 1/36 1/36 1/36 1/6
計 1/6 1/6 1/6 1/6 1/6 1/6 1

必ずゾロ目が出るギャンブラーのサイコロ

  1 2 3 4 5 6 計
1 1/6 0 0 0 0 0 1/6
2 0 1/6 0 0 0 0 1/6
3 0 0 1/6 0 0 0 1/6
4 0 0 0 1/6 0 0 1/6
5 0 0 0 0 1/6 0 1/6
6 0 0 0 0 0 1/6 1/6
計1/6 1/6 1/6 1/6 1/6 1/6 1
サイコロ1つずつの周辺確率（緑色のセル）に注目すると、どちらのケースでも1から6の目が1/6ずつ出ていますが、2つのサイコロを組み合わせとしてみた場合、同時確率は大きく異なっていることが分かります。同じ周辺確率でも、コピュラによって様々な同時確率を作ることが可能になります。 複数の確率変数をモデル化する場合、それぞれの依存性や相関関係をコピュラを用いて精緻に表現することが重要になります。例えば、日本で地震が発生するリスクと株価が下落するリスクには強い依存性があると考えられます。リスクモデル上はコピュラを用いることでこれらのリスク間の依存性を精緻に表現することが考えられます。

参考文献、サイト　Reference

このプログラムは下記の文献、サイト等を参考に作成しています。

Copula全般
https://www.imes.boj.or.jp/japanese/kinyu/2005/kk24-b2-3.pdf
https://beta.vu.nl/nl/Images/werkstuk-mahfoud_tcm235-277460.pdf

Clayton copula
http://web.cecs.pdx.edu/~cgshirl/Documents/Research/Copula_Methods/Clayton%20Copula.pdf

Gaussian copula
https://www.stat.ncsu.edu/people/bloomfield/courses/st810j/slides/copula.pdf

JStat（正規分布やt-分布の分布関数の計算に使用）
jstat.github.io

Gamma function（javascriptによるガンマ関数の近似例）
www.w3resource.com

作ってみた感想

・はてなブログはjavascriptには対応しているものの、コードだけ書かれたシンプルな記事は作成できない仕様らしい。記事を成立させるためにはある程度の長さの日本語を書く必要があり、最後に蛇足的に感想を並べて締めくくります。

・当たり前の話ではあるけれど、同じ相関係数のtコピュラと正規コピュラの結果を比較すると、tコピュラを使用した場合の方が標準正規分布の裾が厚いことが確認できた。

・一方でアルキメデスコピュラはおおむね予想通りの結果となった。Wikipediaを参照すると、アルキメデスコピュラには教科書に記載されている種類以外にも様々な種類があることがわかった。余力があれば追加したい。

・同じ周辺分布でもコピュラに応じて様々なパターンが作れることが分かった。教科書上で2次元のグラフだけで見るよりも、イメージがわきやすいのではないかと思われる。

・欲を言えば３Dプロットのところは確率密度だけでなく、周辺分布も同時に表示できるようにしたい。plotlyのグラフィックスで対応できるかは不明だが、3D表示は難しいかもしれない？もし周辺分布があれば、裾従属係数をビジュアル的に表現するのが容易かもしれない。現状の表示だと裾従属係数が0かどうかは明確でない。

・今回のプロット作成は確率密度の理論値をメッシュごとに計算して作成しているだけだが、実データからのパラメータ推定やシミュレーション（乱数発生）の実装にはもう少し理解を深める必要がありそう。RやPythonではパッケージを利用できるものの、中身はよく理解できていない。シミュレーションができるとVaRの数値計算が可能になり、裾の厚さがより分かりやすくなると思われる。

・多変数の従属性を表現するのに使われるVine Copulaについてもよく理解できていないので、余力があれば実装してみたい。

・コピュラの分布関数を微分して確率密度関数にするのはなかなか骨が折れた。今回は2変数なので自力で完遂できたものの、変数が多い場合のコーディングをするのは難易度が高そう。

・ブラウザ上でインタラクティブに使えるプログラムを作るのが非常に面白く感じるようになった。現在はjavascriptとplotlyの組み合わせしか試せていないが、他にも便利な方法があれば試してみたい。

・リファレンスに記載しているJStatは統計処理ライブラリとして大変便利だった。一点言うとすれば、多変量の正規分布、t分布の分布関数、確率密度関数が提供されていないのは物足りなかったが、他には全く問題なかった。Simple Statisticsと合わせて併用するようにしたい。

「二度あることは三度ある」確率はXX%【ベイズ推定入門】

データサイエンス

本記事はベイズ推定の入門記事です。ベイズ推定を用いて「二度あることは三度ある」確率を定量的に評価し、どんな場合に「三度目の正直」の方が信頼できるかを明らかにします。

  • １．ベイズ推定でできること
  • ２．「二度あることは三度ある」確率
    • ２．１．全く見当がつかない場合
    • ２．２．ある程度見当がついている場合
  • ３．ベイズ推定とベイズの定理
  • ４．ベイズの定理の意味するところ
  • ５．「二度あることは三度ある」確率 VS 「三度目の正直」の確率
  • ６．最尤推定との比較とベイズ推定の利用方法

１．ベイズ推定でできること

日本語には「二度あることは三度ある」、「三度目の正直」という一見すると矛盾したことわざがあります。国語の授業で勉強した際に、どちらが正しいのか疑問に思った方も多いのではないでしょうか。

これらのことわざは「同じ事象が２度繰り返された」という状況において全く逆の示唆を与えますが、その使い分けは話者にどれだけ自信があるかに依存しています。

例えば、４番打者のＡさんが２打席連続で三振したときには、次の打席こそヒットを打つという意味を込めて「三度目の正直」を用いるでしょうし、反対にうっかり者のBさんが２回連続で宿題を忘れていたら「二度あることは三度ある」を使うことになるでしょう。

このように私たちがことわざを使い分ける際には、「４番打者が三振する確率は低い」、「うっかり者は宿題を忘れやすい」といった「主観」をベースに「同じ事象が２度繰り返された」という「情報」を織り込んで確率を評価しています。

このように「主観」と「情報」を用いて確率を定量的に評価するのに適しているのがベイズ推定です。

下図は２パターンの「主観」に基づきベイズ推定を行った例になります。

ベイズ推定では「主観」に「情報」を織り込んで確率を評価することができる
上段は平均25%失敗するという「主観」を持つ場合の一例、下段は平均75%失敗するという「主観」を持つ場合の一例を示します。

それぞれの「主観」に２連続で失敗したという「情報」を織り込むと、「主観」を示す水色の分布は右へシフトし、オレンジ色の分布へと変化します。この右へのシフトは失敗する確率が高く評価されるようになったことを意味しています。

上段は平均33%失敗するという「評価」へ、下段は平均78%失敗するという「評価」へ変化しています。このように「主観」の違いによって「評価」が分かれてしまうことが見て取れます。

今回はこのようなベイズ推定を利用して、「二度あることは三度ある」確率と「三度目の正直」となる確率を比較してみます。

続きを読む

アクチュアリー試験の合格率を予測してみた

アクチュアリー試験

今回の記事では2019年度のアクチュアリー試験の合格率や受験者を予想してみます。

受験生の間では「今年度はあの科目が難化した」「昨年度は合格率が低かったから今年は易化するだろう」といった噂を耳にすることがありますが、将来の合格率を合理的に予測することは可能なのでしょうか？今回は時系列分析等を用いて検証してみます。（あくまで個人的見解・予測であり、実際のアクチュアリー試験の合格率を保証するものではありません）

１．使用するデータ

アクチュアリー・ゼミナールさま掲載のデータを孫引きし、下記リンクの通りデータを集計しました。合格率の分子は各年度の合格者数、分母は各年度の受験者数※になります。（※受験者数＝申込者数－欠席者数であり、受験者全体の数とは異なるようです）

また、年度や科目によっては合格点が60点から調整されていることがありますが、今回の分析では特段のデータ補整は行いません。

２．データ概要

各年度の合格率の推移を表とプロットで表してみます。

 2010~2018

  H22 H23 H24 H25 H26 H27 H28 H29 H30
  2010 2011 2012 2013 2014 2015 2016 2017 2018
数学 11.9% 11.1% 46.8% 18.4% 26.5% 20.2% 19.7% 10.3% 13.0%
生保 35.3% 12.6% 49.2% 26.5% 10.2% 14.0% 10.6% 26.2% 12.8%
損保 12.8% 10.5% 39.9% 30.1% 22.6% 20.5% 13.2% 13.7% 23.5%
年金 11.6% 8.1% 46.8% 58.2% 10.2% 18.5% 16.6% 16.4% 35.2%
KKT 18.8% 20.5% 47.6% 20.3% 22.0% 46.1% 17.2% 19.0% 14.1%

2001~2009

  H13 H14 H15 H16 H17 H18 H19 H20 H21
  2001 2002 2003 2004 2005 2006 2007 2008 2009
数学 9.7% 17.1% 17.7% 6.8% 7.2% 10.6% 41.8% 22.8% 18.9%
生保 29.5% 9.7% 22.5% 7.0% 10.2% 11.0% 38.7% 21.9% 21.5%
損保 29.6% 15.2% 18.1% 22.7% 9.9% 11.9% 13.1% 36.6% 10.5%
年金 14.5% 19.5% 12.4% 11.4% 18.9% 11.9% 52.0% 18.1% 11.6%
KKT 17.6% 34.3% 30.1% 11.5% 23.0% 15.3% 24.8% 27.1% 15.1%

 

f:id:r_std:20200324081630p:plain

2001~2018年の合格率の推移

f:id:r_std:20190602035215p:plain

2001~2018年の合格率の推移（ロジット変換後）

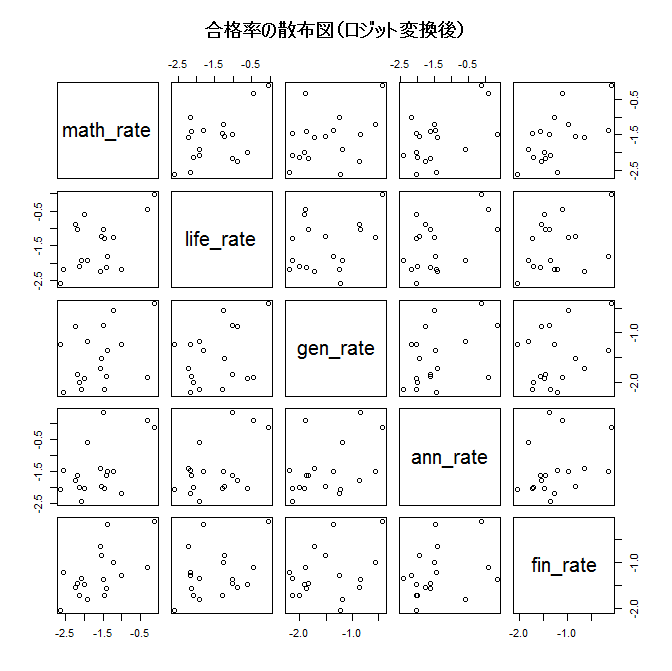
ロジット変換後の時系列データの方が正規分布へのあてはまりが良いことから、今回はロジット変換後のデータを中心に分析します。

※別途正規分布のあてはまりを確認するためシャピロ・ウィルク検定を行っていますが、結果は割愛します。年金数理だけは合格率が上振れした年の影響が強く、正規分布に従う仮定はあてはまりにくいようです。

３．（仮説１）将来の合格率は過去の合格率に左右される？

ここでは将来の合格率が過去の合格率の影響を受けるか否かを、偏自己相関係数を算出して検証します。

合格率が高い状況が続きにくい（難化→易化or易化→難化を繰り返す）場合、偏自己相関係数は負になりやすいと考えられます。

下図はロジット変換後合格率のロジット変換後の偏自己相関係数を表したものです。横軸のLagは過去何年前との自己相関かを示しており、点線は有意水準5%の棄却域を示しています。偏自己相関係数が点線の有意水準を上回る/下回る場合、過去の科目の合格率の影響を受けやすいことが示唆されます。

f:id:r_std:20190602021807p:plain

ロジット変換後データの偏自己相関①

f:id:r_std:20190602021859p:plain

ロジット変換後データの偏自己相関②

有意な自己相関がほとんど観測されないことから、将来の合格率は過去の合格率に左右されるとは言えないと結論づけられます。（なお、ロジット変換前の合格率を使用した場合にも同じ結果が導かれます）

「去年は難化したから今年は易化する」という説は前期比の観点でみれば正しかもしれませんが、真の期待合格率が過去実績を踏まえて変化しているというのは言い過ぎなようです。

「あの科目は去年難化していたから今年は簡単になるはず！受験しよう！」というのは誤った戦略であることが示唆されます。

４．（仮説２）年度によって当たり年、外れ年がある？

年度ごとの合格率の推移を見ると、全体的に合格率の高い年、低い年があるように見えます。

f:id:r_std:20190602041934p:plain

5科目平均の合格率

散布図を見ると、同じ年度の各科目の合格率の間には弱い正の相関があることが窺えます。

f:id:r_std:20190602052539p:plain

ピアソンの相関係数を算出したところ、下記のとおり相関係数行列を得ました。（ロジット変換後のデータに対する相関係数です）

　 数学 生保 損保 年金 KKT
数学 100.0%        
生保 53.5% 100.0%      
損保 36.8% 32.4% 100.0%    
年金 55.0% 49.6% 42.3% 100.0%  
KKT 60.9% 33.7% 32.8% 30.5% 100.0%

無相関検定を行ったところ、数学と生保、数学と年金、数学とKKT、生保と年金の間で5%有意水準で帰無仮説（相関係数＝０）が棄却されました。各科目間で全く合格率に相関がない、とは結論付けにくいようです。

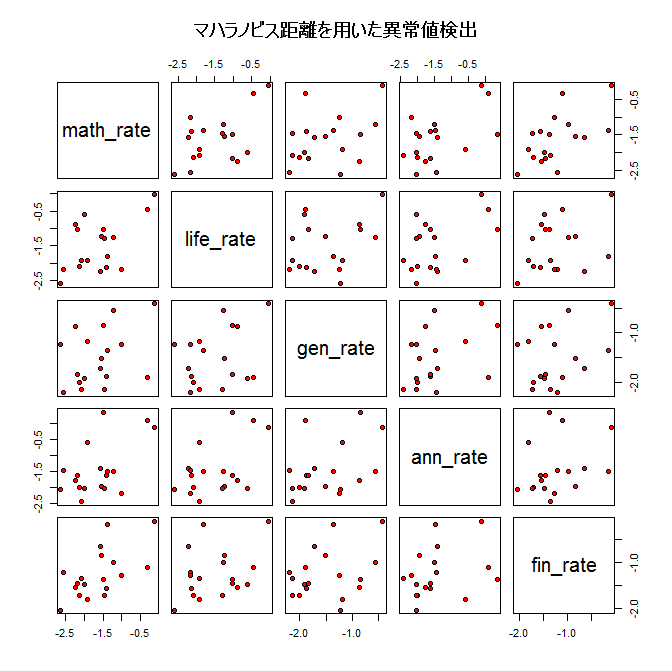
また、相対的に合格率の高い2012年度や2017年が異常値として判定できるかどうか、MT法を用いて異常値検出を行ってみましたが、サンプル数自体が非常に少ないこともあり、マハラビノス距離3では検出することができませんでした。

f:id:r_std:20190602100251p:plain

マハラノビス距離=3では異常値を検出できなかった


５．2019年度アクチュアリー試験の推定合格率

今回はロジット変換後の時系列データが定常な正規分布に従うと仮定して予測を行います。

logit\left( pass\_ rate_{subject,year}\right) \sim N\left( \mu_{subject} ,\sigma_{subject} ^{2}\right)

合格率の最尤推定値は下記の通りとなりました。

数学 生保 損保 年金 KKT
16.5% 18.3% 18.3% 19.2% 22.4%

数学の合格率がやや低く予想されました。

６．（おまけ）将来の受験者数を推定してみる

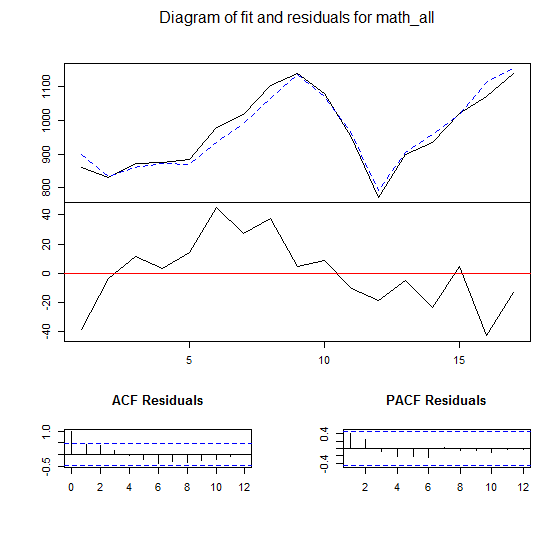
VAR(Vector Auto Regressive)モデルを使って受験者数を予測してみます。VARモデルはARモデルの多変量バージョンです。手法の詳細については こちらのサイトなどをご参照ください。

過去の実績データを用いると、各科目について100人以内の誤差で予測を行うことができました。下記は数学の受験者数の推定モデルの例です。実線が受験者数、破線が推定値を示します。

f:id:r_std:20190602071544p:plain

来年度の受験者数は下記のとおりと予測されます。

  2010 2011 2012 2013 2014 2015 2016 2017 2018 予測
数学 1139 1078 949 773 899 934 1020 1069 1139 1110
生保 813 633 630 554 560 684 753 827 719 816
損保 719 704 641 632 598 615 621 688 652 706
年金 716 754 697 601 440 482 512 542 542 637
KKT 832 784 712 634 660 696 603 733 689 748

 

(2020年3月23日追記) 

Rの実行結果の転記に誤りがありました。正しくは次のとおりです。

  2010 2011 2012 2013 2014 2015 2016 2017 2018 予測
数学 1139 1078 949 773 899 934 1020 1069 1139 1,021
生保 813 633 630 554 560 684 753 827 719 747
損保 719 704 641 632 598 615 621 688 652 663
年金 716 754 697 601 440 482 512 542 542 486
KKT 832 784 712 634 660 696 603 733 689 735

今回使用したデータソースおよびソースコードは次の通りです。 

github.com

exam.R