「二度あることは三度ある」確率はXX%【ベイズ推定入門】
本記事はベイズ推定の入門記事です。ベイズ推定を用いて「二度あることは三度ある」確率を定量的に評価し、どんな場合に「三度目の正直」の方が信頼できるかを明らかにします。
- 1.ベイズ推定でできること
- 2.「二度あることは三度ある」確率
- 3.ベイズ推定とベイズの定理
- 4.ベイズの定理の意味するところ
- 5.「二度あることは三度ある」確率 VS 「三度目の正直」の確率
- 6.最尤推定との比較とベイズ推定の利用方法
1.ベイズ推定でできること
日本語には「二度あることは三度ある」、「三度目の正直」という一見すると矛盾したことわざがあります。国語の授業で勉強した際に、どちらが正しいのか疑問に思った方も多いのではないでしょうか。
これらのことわざは「同じ事象が2度繰り返された」という状況において全く逆の示唆を与えますが、その使い分けは話者にどれだけ自信があるかに依存しています。
例えば、4番打者のAさんが2打席連続で三振したときには、次の打席こそヒットを打つという意味を込めて「三度目の正直」を用いるでしょうし、反対にうっかり者のBさんが2回連続で宿題を忘れていたら「二度あることは三度ある」を使うことになるでしょう。
このように私たちがことわざを使い分ける際には、「4番打者が三振する確率は低い」、「うっかり者は宿題を忘れやすい」といった「主観」をベースに「同じ事象が2度繰り返された」という「情報」を織り込んで確率を評価しています。
このように「主観」と「情報」を用いて確率を定量的に評価するのに適しているのがベイズ推定です。
下図は2パターンの「主観」に基づきベイズ推定を行った例になります。
それぞれの「主観」に2連続で失敗したという「情報」を織り込むと、「主観」を示す水色の分布は右へシフトし、オレンジ色の分布へと変化します。この右へのシフトは失敗する確率が高く評価されるようになったことを意味しています。
上段は平均33%失敗するという「評価」へ、下段は平均78%失敗するという「評価」へ変化しています。このように「主観」の違いによって「評価」が分かれてしまうことが見て取れます。
今回はこのようなベイズ推定を利用して、「二度あることは三度ある」確率と「三度目の正直」となる確率を比較してみます。
2.「二度あることは三度ある」確率
上記の図が示すように、たとえ与えられた「情報」が同じだとしても、前提とする「主観」が異なれば「評価」は大きく異なってしまいます。
ここでは、2種類のパターンを考えてみます。
2.1.全く見当がつかない場合
ここでの「全く見当がつかない」とは、失敗する確率が全く推測できないことを意味します。言い換えれば、失敗する確率が0%から100%のいずれであってもおかしくない場合を仮定します。
この場合、「主観」の分布は平らな分布になります。下の図でみると「主観」を示す水色の分布は一直線となり、山がない状態になっています。

2.2.ある程度見当がついている場合
逆のケースとして、失敗する確率にほぼ見当がついている場合を考えてみます。
例えばコイン投げをして裏が出る確率はほぼ50%と考えられますが、たまたま2回連続で裏が出た場合にも、次に裏が出る確率はやはり50%程度のはずです。
この場合、「主観」の分布は尖っている分布になります。下の図でみると「主観」を示す水色の分布は50%近傍で尖っています。

これらの結果から全く見当がつかない場合には「二度あることは三度ある」確率は75%であることが分かります。
3.ベイズ推定とベイズの定理
ベイズ推定の一例を見ていただいたところで、算出過程を解説します。

これまで、「主観」、「情報」、「評価」と呼んでいたものは、ベイズ統計の言葉に置き換えると、「事前分布」、「観測値(尤度)」、「事後分布」になります。
先ほどの「全く見当がつかない場合」の例に言葉を当てはめると、次の通りになります。

ここでベイズの定理を見てみましょう。
今回の連続分布の例に合わせて書き換えると次のように表すことができます。
この式から、ベイズの定理は事後分布と尤度、事前分布の関係性を示していることが分かります。
これを用いると、先ほどの75%を次の通り導出することができます。
4.ベイズの定理の意味するところ
改めてベイズの定理を眺めてみます。
これを簡略化した書き方は次のようになります。(∝は比例関係を示す記号)
∝
この式からは2つの示唆が得られます。
1つ目は、式の通り求めたい事後分布が尤度と事前分布の積に比例すること。すなわち、求めたい分布は「情報」と「主観」から得られるということ。
2つ目は、求めたい事後分布が観測値の更新によって変化すること。すなわち、観測したデータが増えて「情報」が更新されると、その都度求めたい分布が洗い替えられるということ。こちらはベイズ更新ともいわれ、前述の例では次の図の通りになります。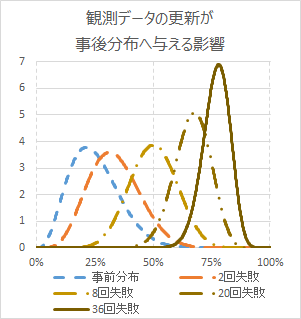
5.「二度あることは三度ある」確率 VS 「三度目の正直」の確率
最後に「三度目の正直」となる確率と「二度あることは三度ある」確率を比較してみます。どのような事前分布を仮定する場合に、「三度目の正直」となる確率の方が大きくなるかを求めます。
「二度あることは三度ある」確率をとすると、
となります。
これが50%を下回ればよいので、事前分布がを満たせば、「三度目の正直」の確率が高いと評価できることが分かります。
この式に定性的な意味づけを与えることは難しいですが、簡単のため「一度あることは二度ある」確率を考えてみると、
が50%を下回れば「二度目の正直」の確率が高いということになります。
の真の期待値である
だけでなく、分散である
も十分に小さい場合、つまり「主観」として持っている失敗する確率が平均もばらつきも十分に小さい場合には「二度目の正直」と言えることが示唆されます。
6.最尤推定との比較とベイズ推定の利用方法
観測データが少ない場合(すなわち「情報」が少ない場合)には、ベイズ推定は利用しやすいと言えます。「二度あることは三度ある」確率 を最尤推定で求めると2/2=100%となってしまいますが、事前分布を設定できるベイズ推定を利用すれば、「主観」を取り入れて柔軟に評価を行うことができます。
ベイズ推定は保険数理においても利用されることがあります。例えば損害保険商品の保険料について、新規契約者と無事故歴の長い契約者との間で較差を設ける際にベイズ統計が利用されることがあります。
ビッグデータの利用が叫ばれる今日ですが、個別ユーザーに関する少量のデータに対しては、ベイズ推定でうまく補完を行うことが重要になるかもしれません。