アクチュアリー試験の合格率を予測してみた
今回の記事では2019年度のアクチュアリー試験の合格率や受験者を予想してみます。
受験生の間では「今年度はあの科目が難化した」「昨年度は合格率が低かったから今年は易化するだろう」といった噂を耳にすることがありますが、将来の合格率を合理的に予測することは可能なのでしょうか?今回は時系列分析等を用いて検証してみます。(あくまで個人的見解・予測であり、実際のアクチュアリー試験の合格率を保証するものではありません)
- 1.使用するデータ
- 2.データ概要
- 3.(仮説1)将来の合格率は過去の合格率に左右される?
- 4.(仮説2)年度によって当たり年、外れ年がある?
- 5.2019年度アクチュアリー試験の推定合格率
- 6.(おまけ)将来の受験者数を推定してみる
1.使用するデータ
アクチュアリー・ゼミナールさま掲載のデータを孫引きし、下記リンクの通りデータを集計しました。合格率の分子は各年度の合格者数、分母は各年度の受験者数※になります。(※受験者数=申込者数-欠席者数であり、受験者全体の数とは異なるようです)
また、年度や科目によっては合格点が60点から調整されていることがありますが、今回の分析では特段のデータ補整は行いません。
2.データ概要
各年度の合格率の推移を表とプロットで表してみます。
2010~2018
| H22 | H23 | H24 | H25 | H26 | H27 | H28 | H29 | H30 | |
|---|---|---|---|---|---|---|---|---|---|
| 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | |
| 数学 | 11.9% | 11.1% | 46.8% | 18.4% | 26.5% | 20.2% | 19.7% | 10.3% | 13.0% |
| 生保 | 35.3% | 12.6% | 49.2% | 26.5% | 10.2% | 14.0% | 10.6% | 26.2% | 12.8% |
| 損保 | 12.8% | 10.5% | 39.9% | 30.1% | 22.6% | 20.5% | 13.2% | 13.7% | 23.5% |
| 年金 | 11.6% | 8.1% | 46.8% | 58.2% | 10.2% | 18.5% | 16.6% | 16.4% | 35.2% |
| KKT | 18.8% | 20.5% | 47.6% | 20.3% | 22.0% | 46.1% | 17.2% | 19.0% | 14.1% |
2001~2009
| H13 | H14 | H15 | H16 | H17 | H18 | H19 | H20 | H21 | |
|---|---|---|---|---|---|---|---|---|---|
| 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | |
| 数学 | 9.7% | 17.1% | 17.7% | 6.8% | 7.2% | 10.6% | 41.8% | 22.8% | 18.9% |
| 生保 | 29.5% | 9.7% | 22.5% | 7.0% | 10.2% | 11.0% | 38.7% | 21.9% | 21.5% |
| 損保 | 29.6% | 15.2% | 18.1% | 22.7% | 9.9% | 11.9% | 13.1% | 36.6% | 10.5% |
| 年金 | 14.5% | 19.5% | 12.4% | 11.4% | 18.9% | 11.9% | 52.0% | 18.1% | 11.6% |
| KKT | 17.6% | 34.3% | 30.1% | 11.5% | 23.0% | 15.3% | 24.8% | 27.1% | 15.1% |


ロジット変換後の時系列データの方が正規分布へのあてはまりが良いことから、今回はロジット変換後のデータを中心に分析します。
※別途正規分布のあてはまりを確認するためシャピロ・ウィルク検定を行っていますが、結果は割愛します。年金数理だけは合格率が上振れした年の影響が強く、正規分布に従う仮定はあてはまりにくいようです。
3.(仮説1)将来の合格率は過去の合格率に左右される?
ここでは将来の合格率が過去の合格率の影響を受けるか否かを、偏自己相関係数を算出して検証します。
合格率が高い状況が続きにくい(難化→易化or易化→難化を繰り返す)場合、偏自己相関係数は負になりやすいと考えられます。
下図はロジット変換後合格率のロジット変換後の偏自己相関係数を表したものです。横軸のLagは過去何年前との自己相関かを示しており、点線は有意水準5%の棄却域を示しています。偏自己相関係数が点線の有意水準を上回る/下回る場合、過去の科目の合格率の影響を受けやすいことが示唆されます。


有意な自己相関がほとんど観測されないことから、将来の合格率は過去の合格率に左右されるとは言えないと結論づけられます。(なお、ロジット変換前の合格率を使用した場合にも同じ結果が導かれます)
「去年は難化したから今年は易化する」という説は前期比の観点でみれば正しかもしれませんが、真の期待合格率が過去実績を踏まえて変化しているというのは言い過ぎなようです。
「あの科目は去年難化していたから今年は簡単になるはず!受験しよう!」というのは誤った戦略であることが示唆されます。
4.(仮説2)年度によって当たり年、外れ年がある?
年度ごとの合格率の推移を見ると、全体的に合格率の高い年、低い年があるように見えます。

散布図を見ると、同じ年度の各科目の合格率の間には弱い正の相関があることが窺えます。
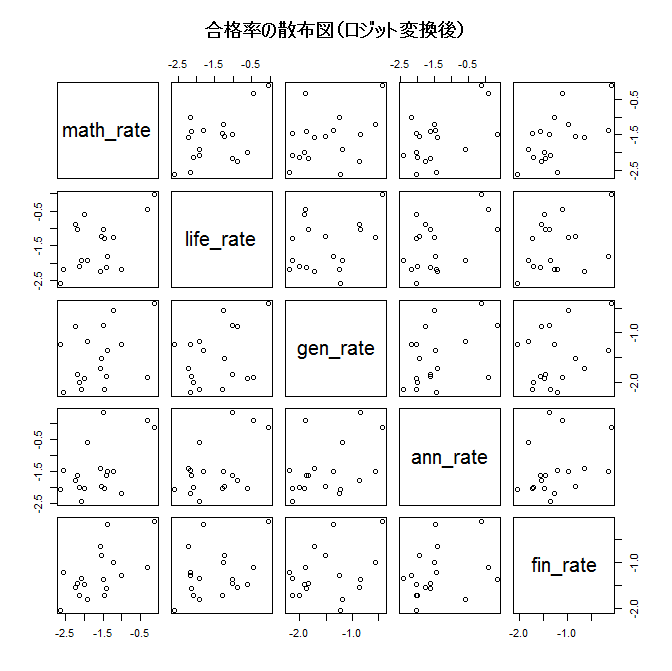
ピアソンの相関係数を算出したところ、下記のとおり相関係数行列を得ました。(ロジット変換後のデータに対する相関係数です)
| 数学 | 生保 | 損保 | 年金 | KKT | |
| 数学 | 100.0% | ||||
| 生保 | 53.5% | 100.0% | |||
| 損保 | 36.8% | 32.4% | 100.0% | ||
| 年金 | 55.0% | 49.6% | 42.3% | 100.0% | |
| KKT | 60.9% | 33.7% | 32.8% | 30.5% | 100.0% |
無相関検定を行ったところ、数学と生保、数学と年金、数学とKKT、生保と年金の間で5%有意水準で帰無仮説(相関係数=0)が棄却されました。各科目間で全く合格率に相関がない、とは結論付けにくいようです。
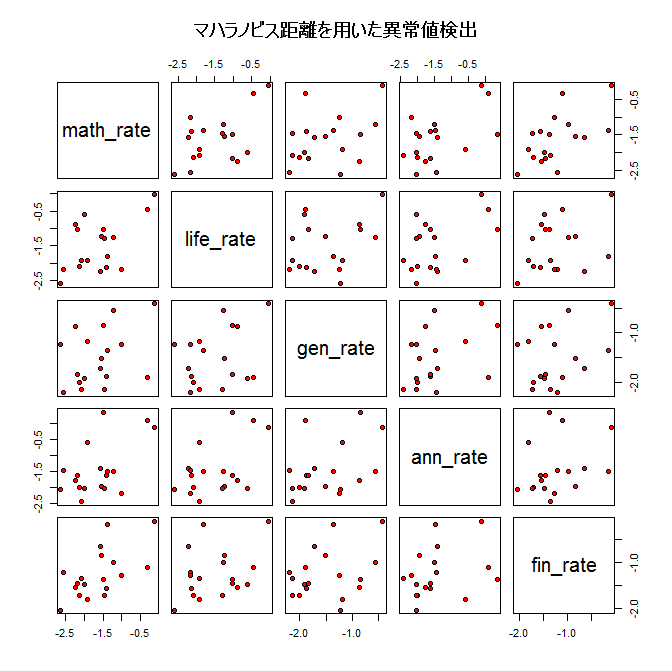
また、相対的に合格率の高い2012年度や2017年が異常値として判定できるかどうか、MT法を用いて異常値検出を行ってみましたが、サンプル数自体が非常に少ないこともあり、マハラビノス距離3では検出することができませんでした。
5.2019年度アクチュアリー試験の推定合格率
今回はロジット変換後の時系列データが定常な正規分布に従うと仮定して予測を行います。
合格率の最尤推定値は下記の通りとなりました。
| 数学 | 生保 | 損保 | 年金 | KKT |
|---|---|---|---|---|
| 16.5% | 18.3% | 18.3% | 19.2% | 22.4% |
数学の合格率がやや低く予想されました。
6.(おまけ)将来の受験者数を推定してみる
VAR(Vector Auto Regressive)モデルを使って受験者数を予測してみます。VARモデルはARモデルの多変量バージョンです。手法の詳細については こちらのサイトなどをご参照ください。
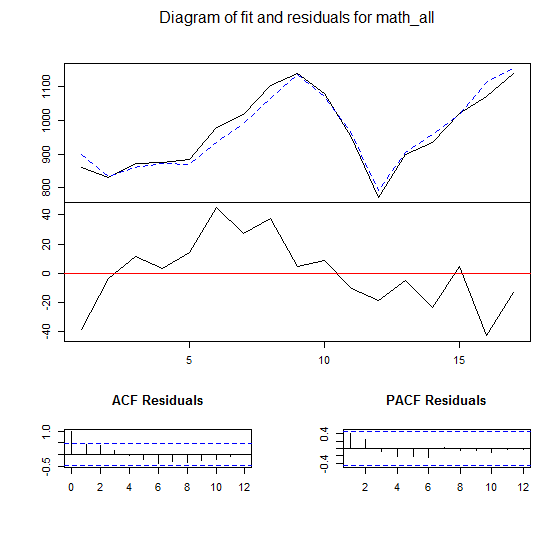
過去の実績データを用いると、各科目について100人以内の誤差で予測を行うことができました。下記は数学の受験者数の推定モデルの例です。実線が受験者数、破線が推定値を示します。
来年度の受験者数は下記のとおりと予測されます。
| 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 予測 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 数学 | 1139 | 1078 | 949 | 773 | 899 | 934 | 1020 | 1069 | 1139 | 1110 |
| 生保 | 813 | 633 | 630 | 554 | 560 | 684 | 753 | 827 | 719 | 816 |
| 損保 | 719 | 704 | 641 | 632 | 598 | 615 | 621 | 688 | 652 | 706 |
| 年金 | 716 | 754 | 697 | 601 | 440 | 482 | 512 | 542 | 542 | 637 |
| KKT | 832 | 784 | 712 | 634 | 660 | 696 | 603 | 733 | 689 | 748 |
(2020年3月23日追記)
Rの実行結果の転記に誤りがありました。正しくは次のとおりです。
| 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 予測 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 数学 | 1139 | 1078 | 949 | 773 | 899 | 934 | 1020 | 1069 | 1139 | 1,021 |
| 生保 | 813 | 633 | 630 | 554 | 560 | 684 | 753 | 827 | 719 | 747 |
| 損保 | 719 | 704 | 641 | 632 | 598 | 615 | 621 | 688 | 652 | 663 |
| 年金 | 716 | 754 | 697 | 601 | 440 | 482 | 512 | 542 | 542 | 486 |
| KKT | 832 | 784 | 712 | 634 | 660 | 696 | 603 | 733 | 689 | 735 |
今回使用したデータソースおよびソースコードは次の通りです。