線形判別分析をRでやってみた(スイス銀行紙幣①)
はじめまして。
当ブログでは小生の独学した内容(主に機械学習)などについて備忘録をかねてまとめていきたいと考えています。多分に誤りが含まれることが予想されますので、お含みおきください。また、先人の皆様にとっては稚拙な内容にはなりますが、至らぬ点についてはご指導頂ければ幸いです。
今回は線形判別分析を用いて、偽札と本物のお札(真札)の分類をやってみます。
1.使用するデータ
使用するデータとしては、次の論文で取りあげられているものを以下のサイトから孫引きします。
Flury, B. and Riedwyl, H. (1988). Multivariate Statistics, A Practical Approach, Cambridge University Press
http://mo161.soci.ous.ac.jp/@d/DoDStat/MethodsList/MultivariateAnalysis_allj.html
上記リンク先の「スイス銀行紙幣データ」を使用します。データの内容は下表のとおりとなっています。
| No | 変数名 | 変数ラベル | 説 明 | 型 |
|---|---|---|---|---|
| 1 | length | 横幅長 | 紙幣の横の長さ | numerical |
| 2 | left | 左縦幅長 | 紙幣の縦の長さ(左側) | numerical |
| 3 | right | 右縦幅長 | 紙幣の縦の長さ(右側) | numerical |
| 4 | bottom | 下枠内長 |
紙幣の下端から内側の枠までの長さ(下部マージン) |
numerical |
| 5 | top | 上枠内長 |
紙幣の上端から内側の枠までの長さ(上部マージン) |
numerical |
| 6 | diagonal | 対角長 | 対角線の長さ | numerical |
| 7 | class | 真偽 | 札の真偽(0: 真札, 1:偽札) | categorical |
データの散布図を図示すると次のとおりになります。

赤色が真札、緑色が偽札を示しています。さて、このデータを基にスイス銀行紙幣の真偽を定量的に判別するにはどうしたらよいでしょうか?
2.線形判別分析とは?
今回取り上げるFisherの線形判別分析は、古典的な機械学習の手法の一つになります。統計ソフトRではMASSパッケージのlda関数を用いることで簡単に行うことができます。
線形判別分析は各群団の中心からの距離(マハラノビス距離)を基準に判別を行う手法です。
今回は線形判別分析を用いて、スイス銀行紙幣のデータを真札群と偽札群の2群に分類します。真札の平均からの距離と偽札の平均からの距離を比較して、距離が小さい方に判別を行います。
次の図は下部マージン(bottom)と対角線の長さ(diagonal)の2変数に絞った場合の線形判別を図示した例になります。
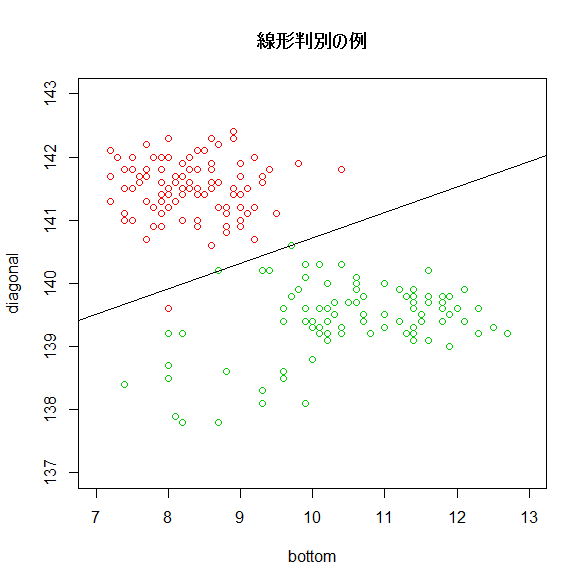
上図の黒線のとおり、識別境界を直線で描くことができました。なお、真札群と偽札群の分布の等高線を描いた場合、下図のとおりとなります。

3.線形判別分析の注意点
線形判別分析は次の2つの前提に基づいている点に注意が必要です。
①各群団が正規分布に従うこと
②全群団が同じ共分散行列を持つこと(等分散性)
②の等分散性を仮定することから、群団ごとの分布の裾の厚薄には対応できないことが線形判別の弱点です。上の散布図でも、真札群と偽札群の分布の等高線が同じ幅、同じ形になっており、等分散性の仮定を用いていることが分かります。
スイス銀行紙幣のデータについては、①の正規分布に従う仮定は問題なさそうですが、②の等分散性についてはやや難があるかもしれません。一般的には偽札の方が製造精度が低く、分散が大きいとが考えられるため、線形判別分析はフィットしづらいのではないかという予想のもと実行してみます。
4.線形判別分析の結果
200件のデータを100件ずつ学習用、テスト用に分けて実行したところ、テスト結果は次の通りとなりました。
> table(test_lda$class,test_y)
test_y
| 真札 | 偽札 | |
|---|---|---|
| 真札 | 49 | 0 |
| 偽札 | 1 | 50 |
等分散の前提に基づく線形判別分析でも、予想に反して判別率99%という良い結果が出ました。 1件だけ真札のデータを偽札であると誤識別してしまっているようです。
5.参考記事・書籍
続編として以下の記事を作成しました。二次判別分析や異常値検出の方法を取り上げています。
今回は下記の書籍を参考にしています。
6.ソースコード
今回使用したソースコードは次の通りです。
