アクチュアリー試験 損保数理の問題をRで解いてみる①

今回は、アクチュアリー試験の問題をRで解きます。

取り上げるのはH25年度の損保数理の第二問Ⅲ　非斉次ポアソン過程の問題です。

 

（１）の答えはオペレーショナルタイムの定義通りなので、上記の通りとなります。tが1/3乗されているため、時間が経過するほど事故が発生しにくくなる設定のようですが、シミュレーションを行うとどのような結果になるでしょうか。 

逆関数法を用いて非斉次ポアソン過程Ntをシミュレーションした一例は次の通りです。題意のパラメータλは３で仮置きしています。t＝100までシミュレーションを行ってみます。

（逆関数法については、こちらなどをご参照ください。）

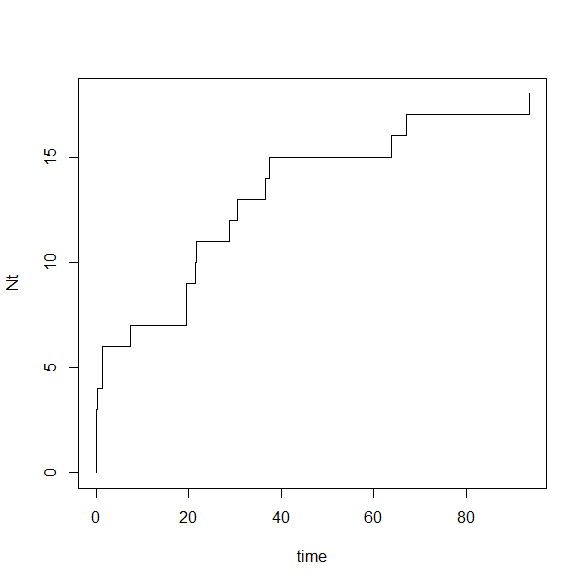
Ntの期待値はt＝27で3×27^(1/3)=9回、t=64で3×64^(1/3)=12回なので、シミュレーションは適切にできているようです。

>||
nhp=function(Tmax,lambda){
u=rep(0,10000)
tau=rep(0,10000)
T=rep(0,10000)

u[1]=runif(1)
tau[1]=-log(u[1])
T[1]=(tau[1]/lambda)^3

u[2]=runif(1)
tau[2]=-log(u[2])+tau[1]
T[2]=(tau[2]/lambda)^3

u[3:10000]=runif(9998)

for(i in 3:100){
 tau[i]=-log(u[i])+tau[i-1]
 T[i]=(tau[i]/lambda)^3
 if(T[i]>Tmax){
 T[i]=0
 break
 }
}
Ti=T[T>0]
N=c(0:length(Ti))
Ti=c(0,Ti)
plot(Ti, N,type = "s",xlab="time",ylab="Nt")
}

nhp(100,3)
||<

数値解を求めてみます。

>||
##n件目の事故がある時刻の平均

ETN=function(m,n,lambda){
result=rep(0,m)
 for(j in 1:m){
 u=rep(0,n)
 tau=rep(0,n)
 T=rep(0,n)

 u[1]=runif(1)
 tau[1]=-log(u[1])
 T[1]=(tau[1]/lambda)^3

 u[2]=runif(1)
 tau[2]=-log(u[2])+tau[1]
 T[2]=(tau[2]/lambda)^3

 u[3:n]=runif(n-2)

 for(i in 3:n){
 tau[i]=-log(u[i])+tau[i-1]
 T[i]=(tau[i]/lambda)^3
 }

 result[j]=T[n]
 }
kekka=mean(result)
return(kekka)
}

ETN(100,5,3)
||<

n=6の場合、5万回シミュレーションした実行結果は次の通りです。

> ETN(50000,6,3)
[1] 12.42624

 6*7*8/3^3=12.444…

(I)が正答だと確認できます。