統計検定準１級に合格しました

先日、統計検定準1級の合格発表がありました。大変うれしいことに評価Sをいただいて合格することができました。引き続き1級の受験も目指して勉強していきたいです。

www.toukei-kentei.jp

試験の難易度としては、アクチュアリー基礎科目の数学をやや難しくしたものに、多変量解析などの専門的なトピックや論述問題が加わったイメージです。直近の2016年6月19日試験での合格率自体は22%となっています。

対策としては、公式問題集と公式サイトの例題集を一周しました。

日本統計学会公式認定 統計検定 1級・準1級 公式問題集[2016〜2017年]

 アクチュアリー試験とあまり関連性のない機械学習分野については、はじめてのパターン認識を読んで知識を補完しました。 

はじめてのパターン認識

 2016年度の試験では、当ブログでとりあげている線形判別分析や、台風の上陸数のモデリングなどが論述問題で出題されたことから、自分にとってはラッキーな出題でした。

試験の開催は年１回6月のようですので、アクチュアリー試験で中だるみを感じている方にはもってこいの試験だと思われます。今年も12月の試験まで150日を切ったようなので、これを皮切りにスパートをかけていきたいと思います。

追記：統計検定準１級の勉強方法についてまとめました。

r-std.hatenablog.com

アクチュアリー試験 損保数理の問題をRで解いてみる①

今回は、アクチュアリー試験の問題をRで解きます。

取り上げるのはH25年度の損保数理の第二問Ⅲ　非斉次ポアソン過程の問題です。

 

（１）の答えはオペレーショナルタイムの定義通りなので、上記の通りとなります。tが1/3乗されているため、時間が経過するほど事故が発生しにくくなる設定のようですが、シミュレーションを行うとどのような結果になるでしょうか。 

逆関数法を用いて非斉次ポアソン過程Ntをシミュレーションした一例は次の通りです。題意のパラメータλは３で仮置きしています。t＝100までシミュレーションを行ってみます。

（逆関数法については、こちらなどをご参照ください。）

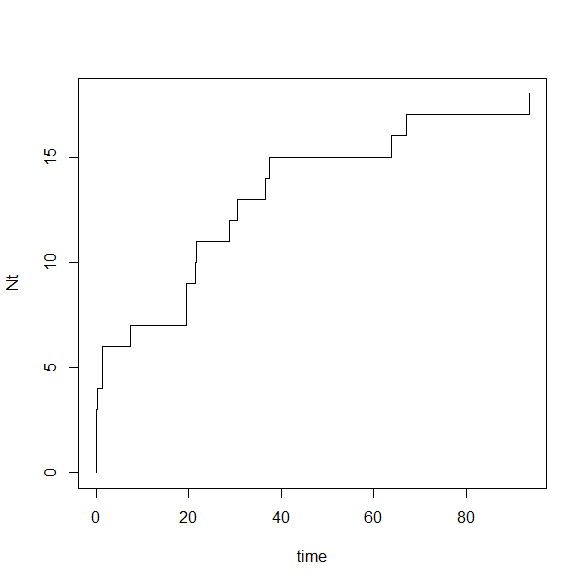
Ntの期待値はt＝27で3×27^(1/3)=9回、t=64で3×64^(1/3)=12回なので、シミュレーションは適切にできているようです。

>||
nhp=function(Tmax,lambda){
u=rep(0,10000)
tau=rep(0,10000)
T=rep(0,10000)

u[1]=runif(1)
tau[1]=-log(u[1])
T[1]=(tau[1]/lambda)^3

u[2]=runif(1)
tau[2]=-log(u[2])+tau[1]
T[2]=(tau[2]/lambda)^3

u[3:10000]=runif(9998)

for(i in 3:100){
 tau[i]=-log(u[i])+tau[i-1]
 T[i]=(tau[i]/lambda)^3
 if(T[i]>Tmax){
 T[i]=0
 break
 }
}
Ti=T[T>0]
N=c(0:length(Ti))
Ti=c(0,Ti)
plot(Ti, N,type = "s",xlab="time",ylab="Nt")
}

nhp(100,3)
||<

数値解を求めてみます。

>||
##n件目の事故がある時刻の平均

ETN=function(m,n,lambda){
result=rep(0,m)
 for(j in 1:m){
 u=rep(0,n)
 tau=rep(0,n)
 T=rep(0,n)

 u[1]=runif(1)
 tau[1]=-log(u[1])
 T[1]=(tau[1]/lambda)^3

 u[2]=runif(1)
 tau[2]=-log(u[2])+tau[1]
 T[2]=(tau[2]/lambda)^3

 u[3:n]=runif(n-2)

 for(i in 3:n){
 tau[i]=-log(u[i])+tau[i-1]
 T[i]=(tau[i]/lambda)^3
 }

 result[j]=T[n]
 }
kekka=mean(result)
return(kekka)
}

ETN(100,5,3)
||<

n=6の場合、5万回シミュレーションした実行結果は次の通りです。

> ETN(50000,6,3)
[1] 12.42624

 6*7*8/3^3=12.444…

(I)が正答だと確認できます。

２次判別分析をRでやってみた（スイス銀行紙幣②）

 本記事では２次判別分析を用いてスイス銀行紙幣の分類を行います。

１．２次判別分析とは

２次判別分析（QDA, Quadratic Discriminant Analysis）は古典的な機械学習の手法の一つであり、前回の記事で解説した線形判別（LDA, Linear Discriminant Analysis）から派生したものになります。

r-std.hatenablog.com

統計ソフトRではMASSパッケージのqda関数を用いることで２次判別分析を簡単に行うことができます。

２．２次判別分析と線形判別分析の違い

線形判別分析には「全群団で分散が等しい」という前提を用いる弱点があります。一方で、２次判別分析では「群団間で分散が異なる」場合にも対応することができます。

前回の記事で取り上げているスイス銀行紙幣の例では、偽札群の分布の分散が真札群よりも大きく、裾が厚くなっていることから２次判別分析の利用が適していると考えられます。 

３．２次判別分析の利用例

前回と同じスイス銀行紙幣のデータについて、２次判別分析を実行していきます。まずは、下部マージン（bottom）と対角線の長さ（diagonal）の２変数に絞って２次判別分析を行った結果を見てみます。

赤色で示した真札群よりも、緑色で示した偽札群の方が分散が大きいことを反映して、青線の通り凸型の識別境界を描くことができました。真札群と偽札群の重心と等高線を描くと下図の通りとなります。等高線の交わるところを識別境界が通っていることが確認できます。

真札と偽札の重心と等高線を追加した散布図

４．２次判別分析の結果

データセットの全変数を用いて２次判別分析を実行した結果は次の通りです。

> table(test_qda$class,test_y)
test_y

	真札	偽札
真札	49	0
偽札	1	50

識別率は99％となり、線形判別と変わらない結果となりました。誤識別されたデータを調べてみます。

ピンク色で示された点が誤識別されたデータになります。真札に含まれる1件の外れ値に対応できなかったようです。

５．２次判別分析の長所・短所

線形判別、２次判別に共通する弱点として、データが正規分布に従うことを前提とする点が挙げられます。スイス銀行紙幣のデータでは各群団がまとまって分布していたため、非常に精度の高い結果を得ることができましたが、データが正規分布に従わず、一様に分布しているケースなどでは、狙い通りの境界を引けない危険性があります。

契約者から取得したデータを保険料率に織り込むことを考える場合、判別分析は汎化能力に優れ、かつ契約者の理解を得られやすいと考えられるものの、コストやプライバシーの観点からどの変数を取得・利用するかが論点になると予想されます。

６．関連記事・参考書籍・ソースコード

続編として、以下の記事を作成しました。

r-std.hatenablog.com

 今回は下記の書籍を参考に執筆しています。 

多変量データ解析 (シリーズ“多変量データの統計科学”)

今回使用したソースコードは次の通りです。

QDA

線形判別分析をRでやってみた（スイス銀行紙幣①）

はじめまして。

当ブログでは小生の独学した内容（主に機械学習）などについて備忘録をかねてまとめていきたいと考えています。多分に誤りが含まれることが予想されますので、お含みおきください。また、先人の皆様にとっては稚拙な内容にはなりますが、至らぬ点についてはご指導頂ければ幸いです。

 今回は線形判別分析を用いて、偽札と本物のお札（真札）の分類をやってみます。

１．使用するデータ

使用するデータとしては、次の論文で取りあげられているものを以下のサイトから孫引きします。

Flury, B. and Riedwyl, H. (1988). Multivariate Statistics, A Practical Approach, Cambridge University Press

http://mo161.soci.ous.ac.jp/@d/DoDStat/MethodsList/MultivariateAnalysis_allj.html

上記リンク先の「スイス銀行紙幣データ」を使用します。データの内容は下表のとおりとなっています。

No	変数名	変数ラベル	説　明	型
1	length	横幅長	紙幣の横の長さ	numerical
2	left	左縦幅長	紙幣の縦の長さ(左側)	numerical
3	right	右縦幅長	紙幣の縦の長さ(右側)	numerical
4	bottom	下枠内長	紙幣の下端から内側の枠までの長さ(下部マージン)	numerical
5	top	上枠内長	紙幣の上端から内側の枠までの長さ(上部マージン）	numerical
6	diagonal	対角長	対角線の長さ	numerical
7	class	真偽	札の真偽(0: 真札, 1:偽札)	categorical

 データの散布図を図示すると次のとおりになります。

赤色が真札、緑色が偽札を示しています。さて、このデータを基にスイス銀行紙幣の真偽を定量的に判別するにはどうしたらよいでしょうか？

２．線形判別分析とは？

今回取り上げるFisherの線形判別分析は、古典的な機械学習の手法の一つになります。統計ソフトRではMASSパッケージのlda関数を用いることで簡単に行うことができます。

線形判別分析は各群団の中心からの距離（マハラノビス距離）を基準に判別を行う手法です。

今回は線形判別分析を用いて、スイス銀行紙幣のデータを真札群と偽札群の2群に分類します。真札の平均からの距離と偽札の平均からの距離を比較して、距離が小さい方に判別を行います。

次の図は下部マージン（bottom）と対角線の長さ（diagonal）の2変数に絞った場合の線形判別を図示した例になります。

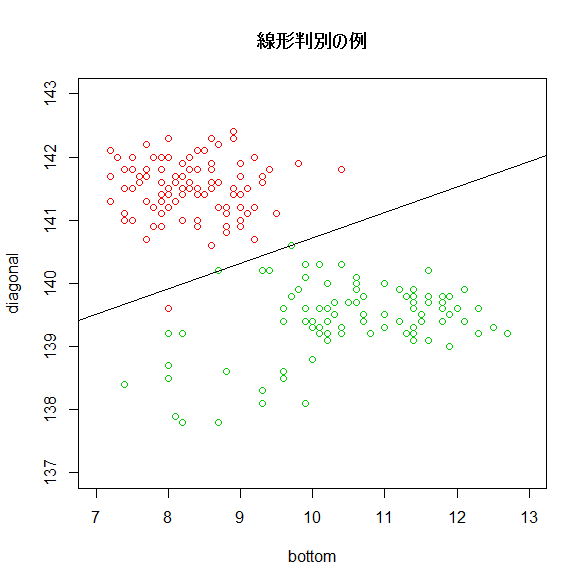
上図の黒線のとおり、識別境界を直線で描くことができました。なお、真札群と偽札群の分布の等高線を描いた場合、下図のとおりとなります。

真札と偽札の重心と等高線を追加した散布図

３．線形判別分析の注意点

線形判別分析は次の２つの前提に基づいている点に注意が必要です。

　①各群団が正規分布に従うこと

　②全群団が同じ共分散行列を持つこと（等分散性）

②の等分散性を仮定することから、群団ごとの分布の裾の厚薄には対応できないことが線形判別の弱点です。上の散布図でも、真札群と偽札群の分布の等高線が同じ幅、同じ形になっており、等分散性の仮定を用いていることが分かります。

スイス銀行紙幣のデータについては、①の正規分布に従う仮定は問題なさそうですが、②の等分散性についてはやや難があるかもしれません。一般的には偽札の方が製造精度が低く、分散が大きいとが考えられるため、線形判別分析はフィットしづらいのではないかという予想のもと実行してみます。

４．線形判別分析の結果

200件のデータを100件ずつ学習用、テスト用に分けて実行したところ、テスト結果は次の通りとなりました。

> table(test_lda$class,test_y)
test_y

	真札	偽札
真札	49	0
偽札	1	50

等分散の前提に基づく線形判別分析でも、予想に反して判別率99%という良い結果が出ました。 １件だけ真札のデータを偽札であると誤識別してしまっているようです。 

５．参考記事・書籍

続編として以下の記事を作成しました。二次判別分析や異常値検出の方法を取り上げています。

r-std.hatenablog.com

 今回は下記の書籍を参考にしています。

多変量データ解析 (シリーズ“多変量データの統計科学”)

６．ソースコード

今回使用したソースコードは次の通りです。 

LDA

お問い合わせ

プライバシーポリシー

当サイトに掲載されている広告について

当サイトでは、第三者配信の広告サービス（Googleアドセンス、Amazonアソシエイト）を利用しています。
このような広告配信事業者は、ユーザーの興味に応じた商品やサービスの広告を表示するため、当サイトや他サイトへのアクセスに関する情報 『Cookie』(氏名、住所、メール アドレス、電話番号は含まれません) を使用することがあります。
またGoogleアドセンスに関して、このプロセスの詳細やこのような情報が広告配信事業者に使用されないようにする方法については、こちらをクリックしてください。

当サイトが使用しているアクセス解析ツールについて

当サイトでは、Googleによるアクセス解析ツール「Googleアナリティクス」を利用しています。
このGoogleアナリティクスはトラフィックデータの収集のためにCookieを使用しています。
このトラフィックデータは匿名で収集されており、個人を特定するものではありません。
この機能はCookieを無効にすることで収集を拒否することが出来ますので、お使いのブラウザの設定をご確認ください。
この規約に関して、詳しくはこちら、またはこちらをクリックしてください。

当サイトへのコメントについて

当サイトでは、スパム・荒らしへの対応として、コメントの際に使用されたIPアドレスを記録しています。
これはブログの標準機能としてサポートされている機能で、スパム・荒らしへの対応以外にこのIPアドレスを使用することはありません。
また、メールアドレスとURLの入力に関しては、任意となっております。
加えて、次の各号に掲げる内容を含むコメントは管理人の裁量によって承認せず、削除する事があります。

　・特定の自然人または法人を誹謗し、中傷するもの。
　・極度にわいせつな内容を含むもの。
　・禁制品の取引に関するものや、他者を害する行為の依頼など、法律によって禁止されている物品、行為の依頼や斡旋などに関するもの。
　・その他、公序良俗に反し、または管理人によって承認すべきでないと認められるもの。

免責事項

当サイトで掲載している画像の著作権・肖像権等は各権利所有者に帰属致します。権利を侵害する目的ではございません。
記事の内容や掲載画像等に問題がございましたら、各権利所有者様本人が直接メールでご連絡下さい。確認後、対応させて頂きます。
当サイトからリンクやバナーなどによって他のサイトに移動された場合、移動先サイトで提供される情報、サービス等について一切の責任を負いません。
当サイトのコンテンツ・情報につきまして、可能な限り正確な情報を掲載するよう努めておりますが、誤情報が入り込んだり、情報が古くなっていることもございます。
当サイトに掲載された内容によって生じた損害等の一切の責任を負いかねますのでご了承ください。

運営者：Yuki
初出掲載：2019年6月10日